Linear mixed model
Linear Mixed Models (LMMs) are statistical models for continuous outcome variables in which the residuals are normally distributed but may not be independent or have constant variance. Study designs leading to data sets that may be appropriately analyzed using LMMs include
- Studies with clustered data, such as students in classrooms, or experimental designs with random blocks, such as batches of raw material for an industrial process, and
- Longitudinal or repeated-measures studies, in which subjects are measured repeatedly over time or under different conditions.
These designs arise in a variety of settings throughout the medical, biological, physical, and social sciences. LMMs provide researchers with powerful and flexible analytic tools for these types of data. Although software capable of fitting LMMs has become widely available in the past decade, different approaches to model specification across software packages may be confusing for statistical practitioners.
Definitions
- Mixed models extend the linear model by allowing a more flexible specification of the errors (and other random factors). Hence, it allows for a different type of inference and also allows to incorporate correlation and heterogeneous variances between the observations.
- Fixed effects: are those factors whose levels are selected by a nonrandom process or whose levels consist of the entire population of possible levels. Inferences are made only to those levels included in the study.
- Random effects: a factor where its levels consist of a random sample of levels from a population of possible levels. The inference is about the population of levels, not just the subset of levels included in the study.
- Mixed linear models contain both random and fixed effects.
The general form of the linear mixed model (in matrix notation) is:
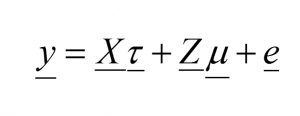
Where,
τ is the vector of fixed effects,
X is a design matrix of fixed effects,
u is the vector of random effects,
Z is the design matrix of random effects,
e is the vector of residual errors.
Assumptions:

The Home Field Advantage (HFA) hypothesis, the state that plants create specific conditions which increase the rate of decomposition of their own litter.
The HFA hypothesis for litter composed of leaves and roots of tropical tree species (Acacia mangium and Eucalyptus grandis) was tested using complete randomized design with three blocks.
ASreml was used for linear mixed model.
Find the original publication
L. R. Bachega, J.-P. Bouillet and others, Forest Ecology and Management, Volume 359, 2016, Pages 33–43.
